「暗号技術 - RSA について」

昨年(平成17年)には、個人情報保護法が施行されるなど以前にも増して秘密を守るということの重要性がクローズアップされてきています。そのような中で使われている技術として暗号化技術があります。
今回は、現在一般的に使用されている暗号化技術のなかでRSA暗号化を取り上げてみたいと思います。普段は意識することはありませんが、身近なところでは普通に買い物に使用するクレジットカードの情報を取り扱うときなどにもRSAは活用されていますので、その動作を少し見てみましょう。

RSAは3人の開発者の頭文字を取って付けられた名前のため、その技術内容とは全く関連性がありません。RSAは公開鍵暗号アルゴリズムの1つです。
公開鍵？秘密にしたいのに鍵が公開されている？少し違和感を感じます。
普通に暗号化を考えた場合、何かしら暗号化したいものがあって、それをある鍵を使って暗号化する。そしてその鍵を使って復号化するとなります。この形式を対称暗号アルゴリズムと呼びます。
これに対して、公開鍵暗号アルゴリズムでは、暗号化する鍵と復号化する鍵は違うものを使用します。そして暗号化する鍵の方は公開してしまいます。
対称暗号アルゴリズムでは暗号化する側に鍵をなんらかの方法で通知する必要がありますが、公開鍵暗号アルゴリズムでは、復号化の鍵は暗号化する側に通知する必要がありません。暗号化鍵を知られたところで復号化の鍵を知らない限り復号化できないのですから意味がありません。

対称暗号アルゴリズム：

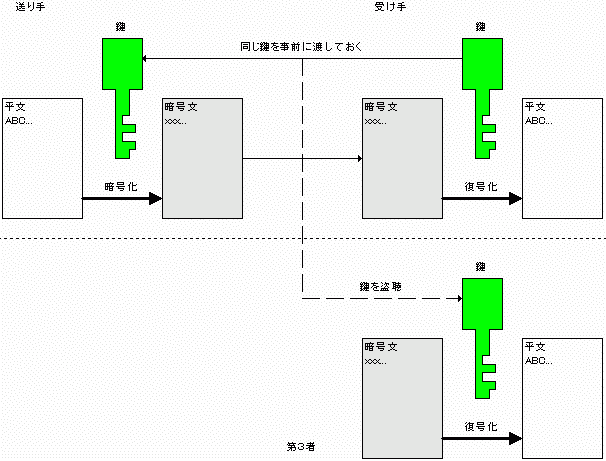
事前に復号化にも使用する鍵を渡す必要があるため、その時点で鍵を盗聴される可能性があります。盗聴された（した）鍵を使用することにより情報を復号化できるので情報が漏洩してしまいます。

公開鍵暗号アルゴリズム：

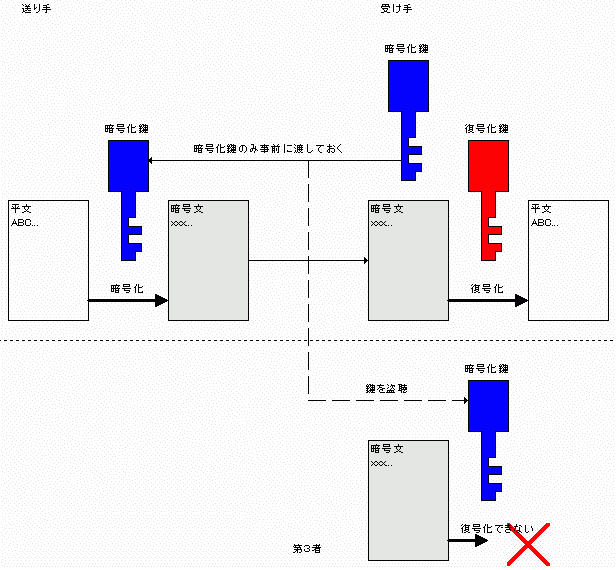
事前に渡す必要がある鍵は暗号化に使用する鍵のみです。その時点で鍵を盗聴される可能性は同様にあります。しかし盗聴された（した）鍵は暗号化専用であり復号化に使用することはできません。よって情報の漏洩を防ぐことができます。

RSAの暗号化／復号化式は以下のように非常にシンプルなものです。

暗号化

復号化

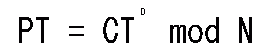
以下で記号を説明します。
CT：暗号文、PT：平文となっており、それぞれなんらかの式の結果、暗号化および復号化されることを示しています。
はじめに、E：公開鍵（暗号化に必要）、D：秘密鍵（復号化に必要）となっており、対象のべき乗をとるという演算を行います。
次に mod N となっていますので、先ほどの値を N で割った余りを求めます。
これだけで、暗号化もしくは復号化が完了します。

実際に値を決めて動きを追うと以下のようになります。
ここでは、以下の値としています。

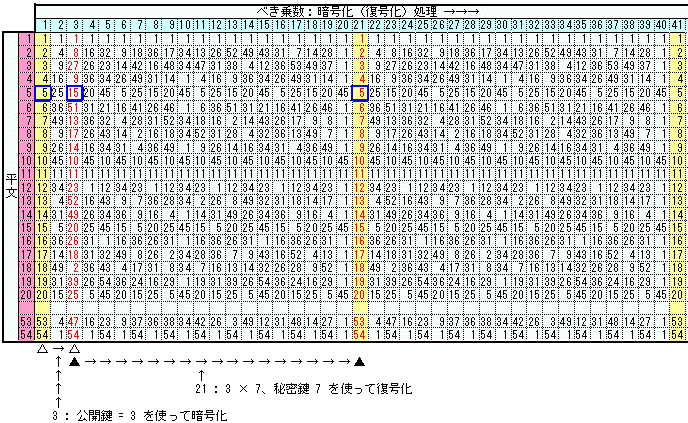
縦が暗号化対象となる平文、横がべき乗数となります。また、ある数（鍵）でべき乗することが暗号化（復号化）することになりますので、横は暗号化（復号化）処理と考えることができます。
ところでべき乗のあとには必ず剰余を取っているので、演算結果は必ず共通鍵 N = 55 以下の値となります。更に表を良くみると演算結果が一定の間隔で繰り返していることが分かります。
具体的な平文 PT = 5 を暗号化→復号化すると以下のようになります。
まず、公開鍵 E = 3 の分だけべき乗して剰余を取ります。これで暗号文 CT = 15 が求められます。次に暗号文 CT = 15 を 21 [公開鍵 E = 3 × 秘密鍵 D = 7] の分だけべき乗して剰余をとります。これが復号化となり、もとの平文 PT = 15 を求めることができます。

難しい原理は少し置いておくとして、上記のような限られた数（共通鍵 N の剰余）の中で演算を繰り返すといずれもとの数字に戻る性質を利用しているということが、なんとなく分かります。
あとはどのようにして、共通鍵 N / 公開鍵 E / 秘密鍵 D を決定すればよいのか？となります。